Understanding fees in eip1559
eip1559 naturally prices congestion most of the time.
In our previous post, this is how we introduced eip1559, a proposal to reform the way users price their inclusion:
In the current system, users attach a bid to their transactions (the gas price), hoping to outcompete other users and entice the next miner enough to include them. However, this first-price auction-style of bidding induces overpayment, UX issues and generally provides few guarantees for inclusion.
With eip1559, a basefee is introduced to price dynamically the congestion endured by the system, setting a minimum entry fee for each block, which in most cases is also the “correct” fee (modulo a small premium). This allows us, as Tim Roughgarden puts it, to move away from difficult-to-gauge transactions looking like buying a house in a dynamic market, towards an Amazon-style, posted price, take-it-or-leave-it paradigm.
To see how the posted-price paradigm is achieved, it’s useful to go in the weeds of how eip1559 determines its quote. It’s in fact possible, even more so than in the current system, to decompose the price quoted under 1559 as the sum of various parts, each arising from specific demand and supply constraints.
The miner fee
In all my writing so far, I’ve emphasised the role of the fee market as a congestion control mechanism to surface the best bids at any given moment. While congestion is responsible for the price variance, there is another cost the transaction fee is paying for. Since this cost is fixed at the timescale of a block, we’ll address it first.
From the perspective of the fee market, miners incur a cost proportional to how much gas they supply: the risk of their block becoming stale. Any extra transaction included in a block slows its propagation and its execution, opening the possibility for the block to not be received or processed in time, before another competing block is.
Ethereum provides rewards for stale blocks if their headers are included on-chain. The stale block miner receives an uncle reward but does not receive any of the transaction fees it included. There are two outcomes for a miner then:
The block is included in the canonical chain and the miner receives the block reward plus the fees attached to included transactions.
The block is “uncled” and the miner receives an uncle reward, smaller than the block reward.
It is estimated that the risk of being uncled is roughly linear in the amount of gas provided: a block twice as large has twice as much chances of not making it into the canonical chain. The miner ought to be compensated for the extra risk they incur by filling a marginal amount of gas in their block. At the limit, we can estimate the cost for a miner to provide one extra unit of gas. Let’s call this marginal cost the miner fee.
It is quite easy to estimate the miner fee. Vitalik has done it some time ago, or more recently you can find this estimation by u/c-i-s-c-o:
The tip level that compensates for uncle risk has been calculated to be about 0.8 gwei (uncle blocks get on average a 1.67 ETH reward instead of the 2 ETH base, so that's a ~0.33 ETH = 330m gwei loss, 10 million gas blocks add ~0.025 to the uncle rate [compared] to empty blocks, so the expected cost of 1 gas is = 330m / 10m * 0.025 = 0.825 gwei) and miners do actually set about this value when the chain is empty.
In a nutshell, it is appropriate to think of the miner fee as compensation for this increased risk of becoming an uncle, and to think of the miner fee as fixed to some nominal value. At this time, the meme appears to be 1 Gwei, based on the estimation above.
The congestion fee
The miner fee embodies the cost of use of the service, borne by the provider. The rest of the fee strictly arises from the cost of congestion, the desire of other users to join the system at the same time. While both costs are somewhat hidden in the fees paid in the current system, eip1559 gives us a much clearer distinction, between the fixed miner fee received as tip and the variable basefee measuring the congestion, in a very precise sense.
Let’s go back to the second-price auction example we introduced in the previous post, where three drivers, A, B and C, were bidding to access a road with limited capacity, fitting only one of the three.
Before driving, we'll have A, B and C write a bid on a piece of paper. There are two rules:
The driver with the highest bid wins the right to use the road.
The winning driver pays the price of the second-highest bid.
Assume all bidders know these rules, but none knows the benefits other drivers obtain from using the road.
The proof is left to you, but it is the case that rational bidders A, B and C ought to bid exactly how much they value the road.
We are looking for a fee that prices out exactly enough users to reach capacity. We saw that charging included users the bid of the first user not accessing the road gave us the efficient solution: users who receive the highest benefits also fill the system to capacity.
eip1559 is kind of a perpetual second-price auction. The basefee floats to price out exactly enough users such that the remaining ones fill the block to capacity. Sometimes it increases (as in English auctions), when the demand is higher than the supply, and sometimes it decreases (as in Dutch auctions), when the demand is lower than the supply.
By the way, what do we mean by demand?

The blue curve represents the demand, the price users are willing to pay for their gas. We order users in decreasing order of willingness. Of course the true demand curve would look a lot more like steps, because a user has a demand for a fixed amount of gas, not just one unit, but you can take this plot as a smooth approximation.
We show one important point: the gas price for which the demand is exactly equal to the block target size of eip1559, 12.5M units of gas. In this example the “equilibrium” price is 50 Gwei: only 12.5M gas worth of users are willing to pay above this price. If basefee was set to 49 Gwei and the miner fee to 1 Gwei, we’d have exactly as much gas in the block as we are targeting.
This is all fine, but since the whole demand curve is way above the miner fee, why couldn’t miners include everyone up to the block limit, set to twice the block target?
Effective demand in eip1559
The reason is that the basefee is binding. Users who do not pay at least the basefee cannot be included. Additionally, users who do not pay the miner at least the miner fee wouldn’t be included.
We'll call effective demand the amount of gas demand by users who are willing to pay at least the basefee plus the miner fee. There are three cases worth taking a closer look at:
Undertarget: The effective demand is lower than the gas target.
Overtarget: The effective demand is higher than the gas target, and lower than the gas limit.
Overfull: The effective demand is higher than both the target and the limit.
Each case maps neatly on the previous plot. If the effective demand is somewhere between 0 and 12.5M gas, we are undertarget. If it is between 12.5M and 25M, we are overtarget. If it is above 25M, we are overfull.
Obviously we’re still aiming for the sweet spot between the under- and overtarget areas, but this is a small window to aim for. So let’s see what happens in each case, starting with the overtarget case.
Overtarget: Effective demand higher than target and lower than limit
In this case, more users can and would be included than the target, meaning that the basefee is too low given the current effective demand. Fortunately, eip1559 allows us a bit of slack in case we haven't exactly figured out the basefee that makes effective demand exactly equal to the gas target.
This slack means users need not overbid. The next block has enough room for all users part of the effective demand. Users are expected to pay exactly the basefee plus the 1 Gwei miner fee.
Overfull: Effective demand higher than target and limit
This case is trickier. The next block cannot accommodate all the effective demand, which is higher than 25M gas. In Roughgarden’s terminology, the basefee is excessively low. In this scenario, it is rational for users to include higher tips with their transactions, to secure their inclusion faster.1
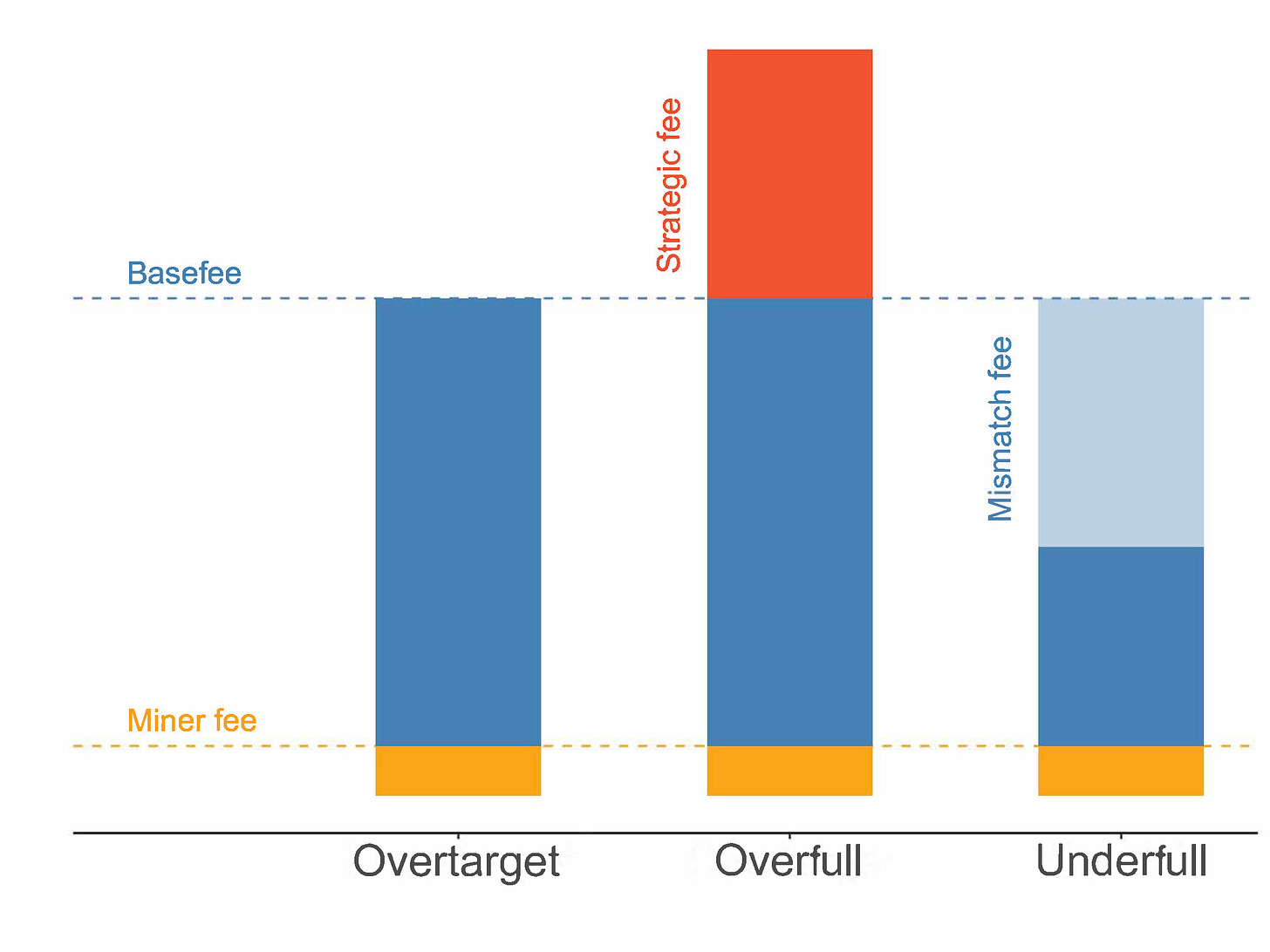
In this case, we decompose the transaction fee in three parts:
The miner fee (1 Gwei).
The basefee, which is not matching the true congestion fee.
The strategic fee, making up for the mismatch.
Although the miner receives parts 1. and 3., the true congestion fee is actually the basefee plus the strategic fee.2
Undertarget: Effective demand is lower than target
In this case, the basefee is higher than it needs to be, pricing out too many users. In the previous case, the true congestion fee was under-estimated by basefee. Now, it is over-estimated, by a quantity we’ll call the mismatch fee. It is still rational for users to bid the basefee + 1 Gwei miner fee strategy.
Fee decomposition in eip1559
As we’ve seen, eip1559 is easily matched to three disjoint cases, each giving rise to specific fee conditions. We summarise them here.
Overall, the user pays the height of each column in the previous plot. The miner receives both the miner fee and the strategic fee, when the latter exists. When blocks are undertarget, the mismatch fee is implicitly contained in the basefee, which hasn’t adjusted downwards yet to meet the decreasing demand.
How often are we in either of these cases? Being under- or overtarget is clearly more desirable than being overfull, since users are simply expected to bid basefee + 1 Gwei miner fee, yielding the elusive UX improvements eip1559 touts. All else equal, effective demand conditions closer to target size are also preferable, since they entail basefee is pricing accurately the congestion, with users paying a fair rate.
There is hope that blocks aren’t usually overfull and that the only tips above basefee + miner fee will come from MEV-extracting transactions. On-chain data after eip1559 is deployed will tell us if we are correct, but in the meantime we can draw more general conclusions on the tension between the basefee update rate and the demand to understand when this fails in theory. In our recent paper, Dynamical Analysis of the EIP-1559 Ethereum Fee Market,3 we go further and prove that chaotic behaviour is observed in the block occupancy rate whenever demand concentrates, producing strong oscillatory behaviour.


We’ll dive into these results in a future entry of this newsletter, subscribe here to be sure not to miss it!
In other 1559 news
1559 is proposed for the London upgrade (probably ~July)
Upcoming 1559 community call (Feb. 26th)


Many thanks to Sacha Saint-Leger for useful comments on this draft.
However, it is not strictly necessary if their time preferences are low, as we’ll see in a future post.
Consider the “tipless” mechanism introduced by Tim Roughgarden (section 8.5). This is always incentive-compatible for the user from the point of view of 1559 (it does not allow for in-protocol strategic overbidding), but now incentivises the user to give the tip to the miner off-chain instead.
Leonardos, S., Monnot, B., Reijsbergen, D., Skoulakis, S., & Piliouras, G. (2021). Dynamical Analysis of the EIP-1559 Ethereum Fee Market. ArXiv, abs/2102.10567.