Congestion control and eip1559
Drawing a more explicit link between congestion games and eip1559 helps frame how fees arise — and where they should go.
eip1559 is a planned upgrade to the Ethereum fee market protocol. In the current system, users attach a bid to their transactions (the gas price), hoping to outcompete other users and entice the next miner enough to include them. However, this first-price auction-style of bidding induces overpayment, UX issues and generally provides few guarantees for inclusion.1
With eip1559, a basefee is introduced to price dynamically the congestion endured by the system, setting a minimum entry fee for each block, which in most cases is also the “correct” fee (modulo a small premium). This allows us, as Tim Roughgarden puts it, to move away from difficult-to-gauge transactions looking like buying a house in a dynamic market, towards an Amazon-style, posted price, take-it-or-leave-it paradigm. In its standard version, eip1559 “burns” the basefee by effectively redistributing it to no one.
Congestion is central to the existence of the fee market and the design of eip1559, and we’ll spend some time defining properly what it means and how we measure it. We’ll see how congestion pricing arises as a fairly natural solution and discuss whether any of its principles help us decide what to do with the fees.
A primer on congestion games
Think of a road with one lane that takes 1 minute to cross if you are alone on the road. Assume that each additional driver on the road increases the travel time by 1 minute. The "latency function" of the road is x, where x is the number of users on the road (so if you are the only driver, the latency is 1 minute).2 How much total travel time does one extra road user bring?
When there is one user A on the road, the total travel time is 1 minute.
When there is one more user B, A now takes 2 minutes to cross the road, and so does B. The total travel time of everyone is 4 minutes.
When there is one more user C, users A, B and C all take 3 minutes to cross the road, so the total travel time is 9 minutes.
In other words, each additional driver adds one extra minute of travel time to all other drivers. If there are 10 drivers on the road and an eleventh driver shows up, the total travel time of these 10 drivers is up 10 minutes (1 minute each). If each driver imposes costs on everyone else, at which point does the overall society lose out?
In search of lost optimality
In algorithmic game theory, we often look for mechanisms that produce the best social outcome given some social dynamics. We’ll start with elaborating what best social outcome means in the context of our drivers, before moving on to the mechanisms that achieve optimality.
We assume the drivers trade-off time and money equally, e.g., spending one extra minute of time on the road is equally as bad as losing a dollar. While all drivers trade-off money and time equally, they receive different benefits from crossing the road. Some drivers want to go to a market they like, but could also choose a different one. Others really need to go see family or attend an important event. For each driver, we associate a number that expresses in dollar terms the benefit they obtain from crossing the road.
Let's take a simple example. We have three road users, A, B and C, with respective benefits $10, $7 and $4 (we’ll drop the $ in the following). If all three users take the road, the travel time for each is 3 minutes. So overall,
A benefits 10 but “pays” 3 minutes of their time on the road, so the profit is 7.
B benefits 7, pays 3, profits 4.
C benefits 4, pays 3, profits 1.
The last number in bold represents the social welfare: how much everybody benefits minus how much everyone pays. Our goal is to make the social welfare as high as possible. Is this the most we can get out of the situation? What if we prevent C from entering at all?
When we prevent C from using the road, we increase the social welfare! Why is this true? The key reason: the extra cost brought on by C to A and B is not compensated by the extra benefit obtained by C. In other words, the private benefit is smaller than the public cost.
We are faced with a clear paradox: there is no reason for C not to enter. Given the information that both A and B plan to use the road, a rational user C would still want to join as well, since they receive one unit of profit, leading to a decrease of the social welfare.
Inducing social optimality: Adding a toll
To obtain the best social outcome, we'd like to operationalise the following idea: any user on the road should pay for the harm it causes other users.3 By internalising the public harm into the private profit evaluation of each user, incentives are aligned. We do so by adding a toll to the road.
How much should the toll charge? We've seen that adding one user to the road when x users are already driving causes x additional cost (1 extra minute per driver). So we should set the toll to x, where x is the number of users already on the road.4 We call this a marginal cost toll, as any incoming user raises the toll to the cost the user imposes on everyone else.
Assume that all users pay x when they are on the road and x users are using it. Suppose A, B and C all enter.
Now C makes a negative profit. They realise it’s just not worth taking the road, so they drop out and we obtain:

Is there some sleight of hand here? We thought the toll would help us reach our socially optimal situation, yet the social welfare is now 9, but it was 13 before! Where did the 4 units go?
In a sense, we have reached the socially optimal outcome (A and B use the road, C doesn't), if not the socially optimal payout (the total profit is 13). The reason is quite simple: 4 units have disappeared into the toll, as both A and B pay 2 units to the toll. We'll discuss this point soon, after making the link with eip1559 clearer.
Constraining the road: Auctions appear
As is probably evident by now, the road is a metaphor for the transaction fee market. Yet our metaphor doesn't really describe the true situation of transactions and blocks. Blocks are limited in size, so they do not allow for unbounded “congestion” the way our model of the road does.
Let's assume that the road only fits one out of our three drivers. Depending on who arrives first, we might have suboptimal situations. For instance, if user C arrives first, the situation is:
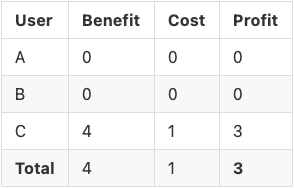
Would a toll work? Well, what if we wanted to target exactly the road capacity, i.e., what if we wanted to induce exactly as many users on the road as the capacity allows for? There is no reason why the socially optimal number of users that the toll returns should be equal to the road capacity. If the toll induces less drivers than the road capacity, arguably we have reached social optimality, so it’s not a problem. But if the socially optimal number of users on the road is above the constraint, the marginal cost toll will not work in general. We’ve seen it already: both A and B were still using the road, which exceeds the capacity we set.
There is a more “essential” reason why a toll cannot in general induce the optimal allocation with capacity constraints. The toll priced the extra latency that a new user imposes on everyone else. With a capacity constraint, a new user doesn’t simply slow down everyone, they totally prevent access to the resource. If we wanted to internalise the public harm via some mechanism, we’d have to price how much this access restriction is worth, beyond the degradation of the service due to congestion.
Fortunately, there is a different mechanism which does just that. We need to think about auctions, specifically, second-price auctions. How should we decide who among A, B and C should access the road?
Before driving, we'll have A, B and C write a bid on a piece of paper. There are two rules:
The driver with the highest bid wins the right to use the road.
The winning driver pays the price of the second-highest bid.
Assume all bidders know these rules, but none knows the benefits other drivers obtain from using the road.
The proof is left to you, but it is the case that rational bidders A, B and C ought to bid exactly how much they value the road. For now, we’ll forget that crossing the road itself is costly for the winning user, and focus on the bids only.5

Another sleight of hand! Where did the 7 dollars A bid go? The answer: in the auctioneer's pocket. But who is the auctioneer? Is the auctioneer the road provider?
🔥🔥🔥
We follow our intuitive definition of internalising public costs: we make users pay for the harm they cause others. If A wasn't there, B should be the driver on the road (to maximise public benefit), while B would harm C by taking the road from them. Congestion thus affects users who were keen to access some resource, but couldn’t, or could at a degraded level of service. Shouldn’t these users be compensated for their loss?
In a monetary economy, there is one way to compensate for the harm caused by congestion that retains efficiency, in the game-theoretic sense of “users with the highest benefits obtain the right to access”: not redistributing the fee to anyone.
This isn't a silver bullet, and it isn't exactly equivalent to redistributing equally the collected fees among everyone, because the mechanics of a monetary economy are a bit more subtle than this. But the intuition is:
Users-as-transaction-senders bear the costs of congestion, since it deprives them of access to the transaction market.
Thus users-as-transaction-senders ought to be compensated for the costs induced by congestion.
The two points above are perhaps the most straightforward microeconomic argument for burning-as-congestion-compensation. Yet, arguing for burning as a necessarily fair microeconomic consequence is difficult for at least two reasons.
Suppose we do believe that burning is an exact redistribution of the amount burned over all participants. In a large economy, this direct redistributive effect is extremely diluted over individual recipients, approaching zero as the number of participants increases (assuming a fixed amount of fees throughout).
Let’s say we are fine with the dilution: an epsilon amount of cash is better than zero after all. We can level a second critique to the microeconomic argument. We've not differentiated, among our population of Ethereum users, between transaction senders and holders. While transaction senders are the ones inconvenienced by the congestion, holders aren't (by definition, they don't send any transactions). But how should a mechanism determine who has been harmed by the congestion or not? Likely, it is impossible, as we’d need to know who would have sent a transaction but didn’t because of the congestion. Is rewarding everyone who holds ETH with the burn a good enough approximation of a mechanism that compensates those affected by the fee market congestion?
I’ve often seen this argument mentioned by miners as a reason why it is delusory to expect that burning achieves redistribution, because of the dilution, and I tend to agree. If this direct, “micro” effect is unsatisfying, perhaps we can think of a more indirect, “macro” effect of the burn that we feel stronger about.
So we decompose the total effect of the burn between a more direct “redistribution effect” of burning part of the supply (with the caveats seen above that this redistribution is both diluted and approximative) and a more indirect effect based on the more intangible nature of ETH as an asset fit to secure the Ethereum network.6
This second, indirect effect tends to be more popular among pro-eip1559 people, and is probably what they mean by “eip1559 will solidify ETH as an asset”, i.e., not something that is measured by comparing inflation pre- and post-eip1559 and scaling the price of ETH by the difference. With the burn proportional to the demand for the network, a link is created between ETH the asset and the network value of Ethereum. In turn, a better ETH increases the bandwidth to use the asset as, e.g., collateral for generating more DAI, in addition to increasing the general level of security of eth2 for instance.
There are other, very good reasons for burning, including weaning off an economy of a highly volatile revenue source which, at the limit, induces instability and complicates miner revenue estimations; recentring the block reward as the mechanism via which security is paid for; or preparing the ground for the transition from Proof-of-Work to Proof-of-Stake.7 Whether any of these ought to apply as soon as eip1559 is turned on versus in months or a year after seems to have indeed become the stage for the argument.
In the next Price of agency
Since we’ve gone to the trouble of defining what we mean by congestion and how to price it, we’ll drop the road metaphors and see how eip1559 brings us closer to that price by inspecting its dynamics. Subscribe to receive it as soon as it is out.
Many thanks to Vitalik Buterin, Sacha Saint-Leger and Tim Beiko for comments and edits. Errors, opinions and erroneous opinions remain mine.
See the introduction of this notebook for the distinction between first-price auctions and eip1559, and this notebook for a comparison between the price induced in the current system and eip1559. And see a whole bunch of other things in Tim Beiko’s resource list.
This type of game is called atomic congestion game: users are “atoms”, or discrete units of mass 1, unlike nonatomic congestion games which feature continuous flows of users, or weighted congestion games where discrete users have different masses. The latency function x is linear.
This is known as a Pigovian tax, named after the economist Arthur C. Pigou.
What would the marginal cost toll be if the latency function was 2x instead of x ? Would B choose to take the road?
To be precise, we should offset the expected cost of using the road from the users’ benefits. Because of the capacity constraint, users should expect to incur a cost of 1 if they are granted access. So A’s true value is their benefit 10 minus 1, in which case they would bid 9 and B would bid 6. In the transaction fee market, the “cost of crossing the road” is 0, so the total costs incurred by the included user are exactly equal to the “bid”.
Both of these statements can be true at the same time: the direct effect isn’t so important and the indirect effect is. This is perhaps one reason why it feels like the two factions sometimes talk past each other.
On this last point, see also the wonderful paper by Leonardos et al. (2020), which “raises the temperature” on the technology to deprecate, until agents make the switch.





good point re: how approximative 1559 is as a redistributor to other tx senders. is there an argument to be made that it's a closer approximation than the status quo (which just pays miners)?
I guess this would assume that miner<>user has less of an intersection than collateral/hodler<>user (...?)